1.
Which of the following sequences of array elements forms a heap?
(a) {23, 17, 14, 6, 13, 10, 1, 12, 7, 5}
(b) {23, 17, 14, 6, 13, 10, 1, 5, 7, 12}
(c) {23, 17, 14, 7, 13, 10, 1, 5, 6, 12}
(d) {23, 17, 14, 7, 13, 10, 1, 12, 5, 7}
Answer
Heap has the following two properties:-
1) All the levels are filled in the order i.e. all the levels have maximum number of nodes except possibly the last level. In the last level all the nodes occur to the left.
2) Heap order property –If it is max heap, then data in root node must be greater than its successors. In case of min heap, then data in root node must be less than its predecessors.
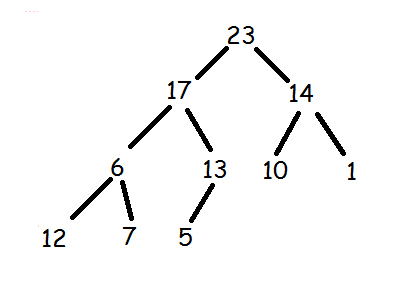
It is not a max heap as 12 and 7 are greater than 6.
But since (c) follows both the property at each node. This is a heap.
A complete binary min-heap is made by including each integer in [1, 1023] exactly once. The depth of a node in the heap is the length of the path from the root of the heap to that node. Thus, the root is at depth 0. The maximum depth at which integer 9 can appear is ________
(a) 2
(b) 3
(c) 8
(d) 9
Answer
1 can be the top node only as it is the smallest node and min heap needs to be formed.2 can become child node of 1,3 can again become child node of 2 and so on. All the other nodes after 9 can be filled in the manner that satisfies structural property of heap ( Complete binary tree). So maximum depth could be 8.
3.
Consider the following array of elements. 〈89, 19, 50, 17, 12, 15, 2, 5, 7, 11, 6, 9, 100〉. The minimum number of interchanges needed to convert it into a max-heap is
(a) 4
(b) 5
(c) 2
(d) 3
Answer
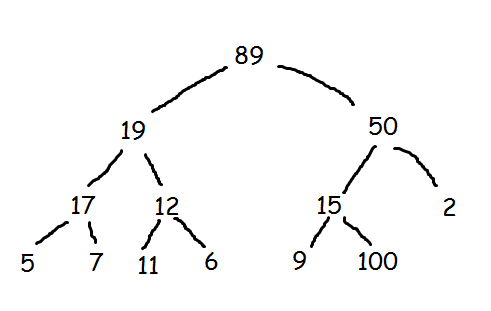
Here in all 3 swaps are required
1) 100 needs to be swapped with 15.
2) 100 needs to swapped with 50
3) 100 needs to be swapped with 89.
This will create a max heap satisfying all the properties of it.
4.
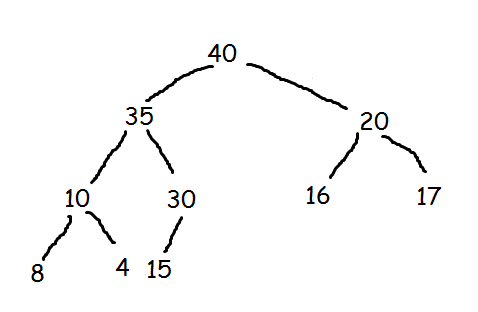
Consider a max heap, represented by the array: 40, 30, 20, 10, 15, 16, 17, 8, 4. Now consider that a value 35 is inserted into this heap. After insertion, the new heap is
(a) 40, 30, 20, 10, 15, 16, 17, 8, 4, 35
(b) 40, 35, 20, 10, 30, 16, 17, 8, 4, 15
(c) 40, 30, 20, 10, 35, 16, 17, 8, 4, 15
(d) 40, 35, 20, 10, 15, 16, 17, 8, 4, 30
Answer
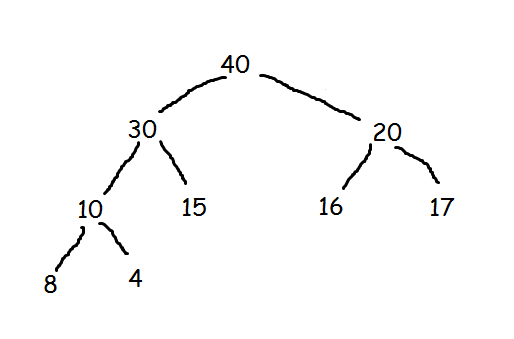
Now 35 is inserted to it at the bottom.
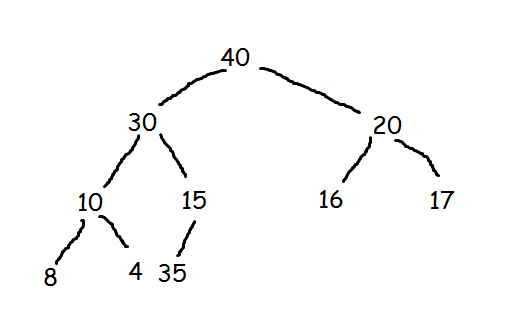
Now restoring it up to again regain the max heap property,two swaps are required
a) Since 15 is smaller than 35, these both needs to be swapped.
b) 30 is less than 15, so again 35 and 15 needs to be swapped.
5.
Consider any array representation of an n element binary heap where the elements are stored from index 1 to index n of the array. For the element stored at index i of the array (i <= n), the index of the parent is
(a) i – 1
(b) floor(i/2)
(c) ceiling(i/2)
(d) (i+1)/2
Answer
If i is the index of child, then floor(i/2) is the index of the parent.In short, if index starts from 1 and parent is at I,then its child if present are at 2i and 2i+1 node.
6.
In a max heap, element with the greatest key is always in the ______________ node
(a) leaf
(b) root
(c) first node of left sub tree
(d) first node of right sub tree
Answer
Heap satisifies structure property and heap order property.Heap property says that parent element should be greater than any of its children. By this logic, we can infer that greates element should be at root.
What is the most appropriate data structure to implement a priority queue?
(a) Heap
(b) circular array
(c) Linked list
(d) Binary tree
Answer
Heap is used to implement priority queue because both insertion or deletion can be done in O(logn) time which is better compared to other data structures.
A complete binary tree with the property that key value in any node is greater than or equal to the key values in both its children is called as.
(a) Binary search tree
(b) Threaded binary tree
(c) Heap
(d) AVL tree
This is the heap order property.
9.
What is the time complexity of Build Heap operation.
(a) O(nLogn)
(b) O(n^2)
(c) O(Logn)
(d) O(n)
Answer
Heap can be built in O(n) time using Bottom up approach.
10.
In a binary max heap containing n numbers, the smallest element can be found in time (GATE CS 2006)
(a) O(n)
(b) O(logn)
(c) O(loglogn)
(d) O(1)
Answer
In the max heap, smallest number can be a leaf node only.Thats why we will have to check all the leaf nodes. Leaf nodes will always be of O(n).
Hence answer is A).
